
기출문제를 통해 "지수"에 대해서 알아보겠습니다!
여러분은 덧셈과 곱셈은 이미 알고 계시죠?
덧셈과 곱셈을 알면 지수를 금방 이해할 수 있습니다.
2+2 는 몇일까요? 4입니다. 금방 계산이 가능하죠?
2+2+2 는 6이죠. 2+2+2+2 는 8이고요.
그럼 2+2+2+2+2+2+2+2+2+2+2+2 는 몇이죠?
금방 계산이 안됩니다. 이것은 머리가 좋고 나쁨을 떠나서
우리 눈에 너무 숫자가 많아보여 복잡해서 그렇습니다.
저런 경우에 우리는 빠르게 계산을 하기 위해 곱셈이라는 개념을 가져옵니다.
더하기 에서 곱하기 로 확장
2를 12번 더했네요. 그러면 2 x 12 라고 쓰면 24라는 답이 금방 계산이 됩니다.
이번엔 곱하기 문제를 풀어보죠.
2 x 2 는 몇일까요? 4입니다.
2 x 2 x 2 = 8 이고 2 x 2 x 2 x 2 = 16 입니다.
그렇다면, 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 는 몇일까요?
이것 또한 숫자가 양옆으로 너무 길어서 우리 눈에 한번에 안 보입니다.
이러한 문제를 해결하기 위해 지수라는 개념을 가져옵니다.
곱하기 에서 지수 로 확장
2를 8번 곱했으니 보기 편하게
\( 2^8 \)
으로 쓸 수 있습니다.
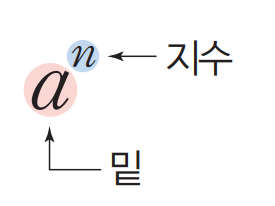
여기서 2 옆에 조그맣게 8이라고 쓰여진 부분을 지수라고 말합니다.
8 밑에 쓰여진 2는 말그대로 밑이라고 부릅니다.
덧셈을 편하게 하기 위해 → 곱셈
곱셈을 편하게 하기 위해 → 지수
이제 지수를 알게 되었습니다.
지수와 관련된 규칙이 몇가지가 있는데 같이 알아보시죠!
2 x 2 = \( 2^2 \) 으로 표현이 가능합니다.
2 x 2 x 2 = \( 2^3 \) 이죠.
그렇다면 \( 2^2 \) x \( 2^3 \) 은 어떻게 표현해야 할까요?
잘 생각해보면
(2 x 2) x (2 x 2 x 2)
2를 두번 곱한 것과 2를 세번 곱한 것을 곱하면
결국
2를 다섯번 곱한 것과 같죠?
그래서 \( 2^2 \) x \( 2^3 \) = \( 2^5 \) 으로 표현이 됩니다.
밑이 같을 때 서로 곱하게 되면
밑은 그대로 두고 지수끼리 더하면 됩니다!

자, 그러면 \( 2^3 \) ÷ \( 2^2 \) 은 어떻게 될까요?
이것도 잘 생각해보면
(2 x 2 x 2) ÷ (2 x 2)
2를 세번 곱한 것을 2를 두번 곱한 것으로 나눠주면
2가 하나만 남네요.
그래서 답은 2가 됩니다.
밑이 같을 때 서로 나누게 되면
밑은 그대로 두고 지수끼리 빼면 됩니다!

이번엔 \( 2^3 \) x \( 2^3 \) 을 간단히 표현해봅시다.
\( 2^3 \) 이 똑같은 것이 두번 곱해졌네요?
지수를 이용해서
\( (2^3)^2 \)
이렇게 표현할 수 있습니다.
저렇게 지수가 연달아서 붙어있는 경우
지수끼리 곱해주면 됩니다.
그래서 \( 2^6 \) 으로 표현이 됩니다.

여기까지 잘 따라오셨다면
드디어 처음 주어진 문제를 풀 수 있게 되었습니다.

답은 5번입니다.
수고하셨습니다.